Avl Tree Search C++
Self-Balancing is provided by painting each node with two colorsRed or Black. The height never grows beyond log N where N is the total number of nodes in the tree.
Avl Tree Set 1 Insertion Geeksforgeeks
Insertion in AVL tree is performed in the same way as it is performed in a binary search tree.
. AVL tree is a self-balancing Binary Search Tree where the difference between heights of left and right subtrees cannot be more than one for all nodes. AVL trees are self-balancing binary search trees. A Binary Search Tree or BST as it is popularly called is a binary tree that fulfills the following conditions.
When the Tree is modified a new tree is subsequently rearranged and repainted. The new node is added into AVL tree as the leaf node. A tree having a right subtree with one value smaller than the root is shown to demonstrate that it is not a valid binary search tree.
AVL tree is a height-balanced tree and therefore the height of the tree never grows more than N where N is the number of nodes in the tree. The rotation operations left and right rotate take constant time as only few pointers are being changed there. AVL tree has capabilities of self-balancing.
There are two basic operations that you can perform on a binary search tree. However it may lead to violation in the AVL tree property and therefore the tree may need balancing. Searching for a specific key in an AVL tree can be done the same way as that of.
It requires 1 bit of color information for each node in the tree. But in red-black we can use the sign of number if numbers being stored are only positive and hence save space for storing balancing information. DFS starts with a root node or a start node and then explores the adjacent nodes of the current node by going deeper into the graph or a tree.
Else check if the item is less than the root element of the tree if this is true then recursively perform this operation with the left of the root. It gives better search time complexity when compared to simple Binary Search trees. AVL tree is a self-balancing binary search tree in which each node maintains an extra information called as balance factor whose value is either -1 0 or 1.
The height of the AVL tree is always balanced. IF TREE NULL Allocate memory for TREE SET TREE - DATA ITEM. Semua simpul-simpul di sub-pohon kiri dari sebuah simpul harus memiliki nilai lebih kecil dibandingkan daripada simpul itu dan semua simpul-simpul di sub.
It is used to. There are even other reasons where redblack is mostly prefered. The binary tree on the right isnt a binary search tree because the right subtree of the node 3 contains a value smaller than it.
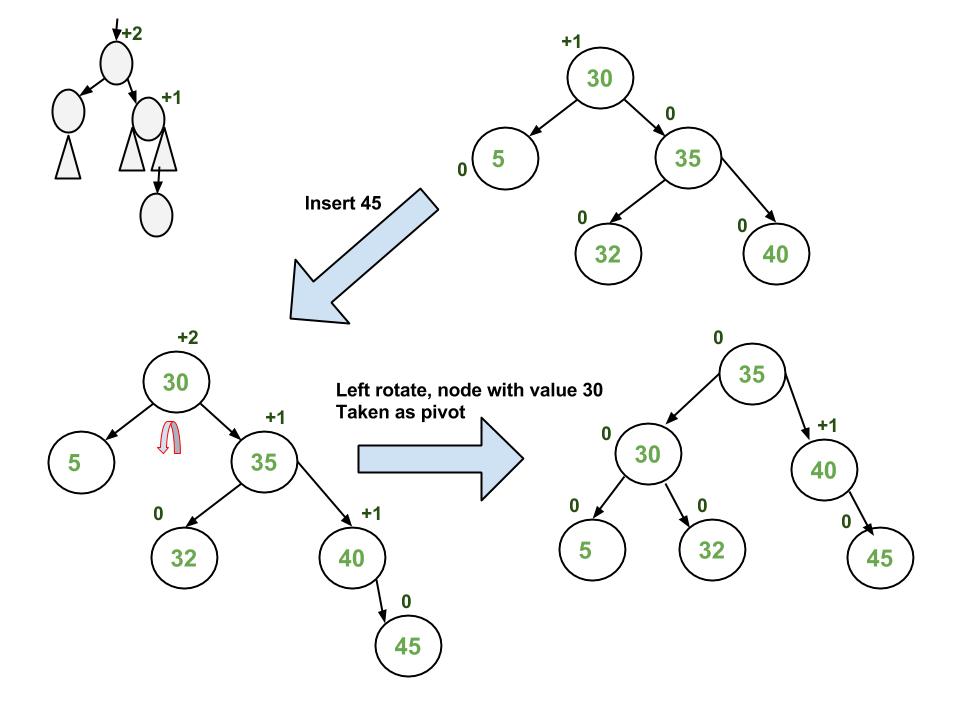
Rotation is required only if the balance. Updating the height and getting the balance factor also take constant time. Every node in an AVL tree need to store the balance factor -1 0 1 hence space costs to On n being number of nodes.
-only operations of an AVL tree involve carrying out the same actions as would be carried out on an unbalanced binary search tree but modifications have to observe and restore the height balance of the sub-trees. This means that in DFS the nodes are explored depth-wise until a node with no children is encountered. Advantages of AVL Trees.
Preorder traversal of the constructed AVL tree is 9 1 0 -1 5 2 6 10 11 Preorder traversal after deletion of 10 1 0 -1 9 5 2 6 11. Detailed Tutorial on Binary Search Tree BST In C Including Operations C Implementation Advantages and Example Programs. A binary tree is defined to be an AVL tree if the invariant.
Depth-first search DFS is yet another technique used to traverse a tree or a graph. The nodes that are lesser than the root node which is placed as left children of the BST. In this tutorial you will understand the working of various operations of an avl-black tree with working code in C C Java and Python.
Constraints maintained by Red Black Tree. Sebuah Pohon Biner Terurut PBT atau biasa disebut Binary Search Tree BST dalam Bahasa Inggris adalah sebuah pohon biner di mana setiap simpul hanya memiliki tidak lebih dari 2 anak yang memenuhi properti BST. It moves one node up in the tree and one node down.
The tree can be balanced by applying rotations. AVL trees have efficient search time complexity. If this is false then perform this operation recursively with the right sub-tree of the root.
Insert TREE ITEM Step 1. Tree rotation is an operation that changes the structure without interfering with the order of the elements on an AVL tree. The time complexity of the AVL tree is faster and constant in comparison to the binary search tree.
AVL trees have self-balancing capabilities.

Avl Tree Set 1 Insertion Geeksforgeeks
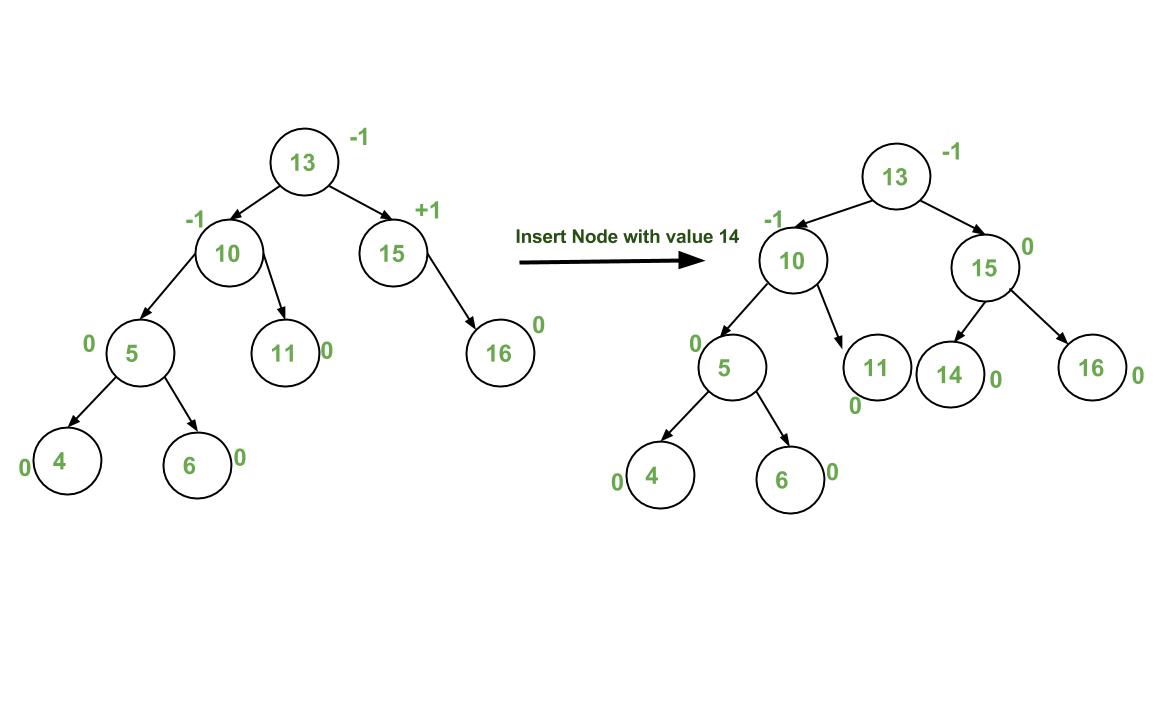
Avl Tree Set 1 Insertion Geeksforgeeks
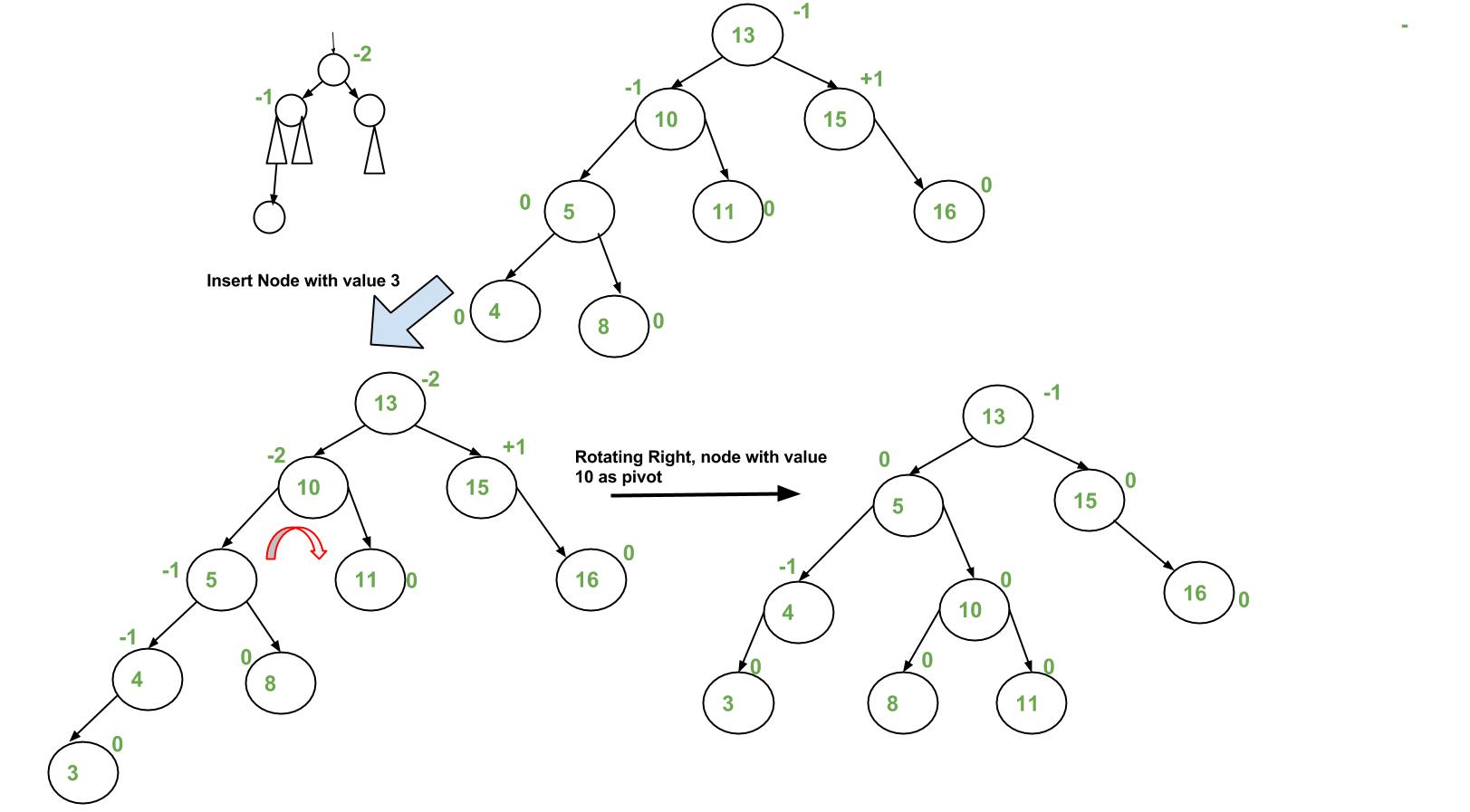
Comments
Post a Comment